Hierarchical Clustering: Intro with Math and Python

Introduction
Clustering is a fundamental task in unsupervised machine learning that involves grouping data points based on their similarities. Hierarchical clustering is a powerful clustering technique that builds nested clusters in a hierarchical manner. This tutorial will walk you through the process of implementing hierarchical clustering using Python, with a practical example using the Mall Customers dataset.
We will cover:
- Understanding hierarchical clustering
- Mathematical foundations of the algorithm
- Preparing the dataset
- Using dendrograms to determine the optimal number of clusters
- Training the hierarchical clustering model
- Visualizing the clusters
Let's dive in!
Understanding Hierarchical Clustering
Hierarchical clustering creates a tree of clusters called a dendrogram. There are two main types:
- Agglomerative Hierarchical Clustering: A "bottom-up" approach where each data point starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive Hierarchical Clustering: A "top-down" approach where all data points start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In this tutorial, we'll focus on agglomerative hierarchical clustering.
Mathematical Foundations of Hierarchical Clustering
Understanding the mathematical basis of hierarchical clustering is crucial for interpreting the results and customizing the algorithm to suit specific needs.
Distance Metrics
At the core of hierarchical clustering is the concept of distance between data points and clusters. The distance metric defines how similarity is measured.
- Euclidean Distance: The most common metric, defined as:[
d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}
]where (\mathbf{x}) and (\mathbf{y}) are two data points in (n)-dimensional space.
Linkage Criteria
The linkage criterion determines how the distance between clusters is calculated based on the distances between the data points within them. Common linkage methods include:
- Single Linkage (Minimum Distance):
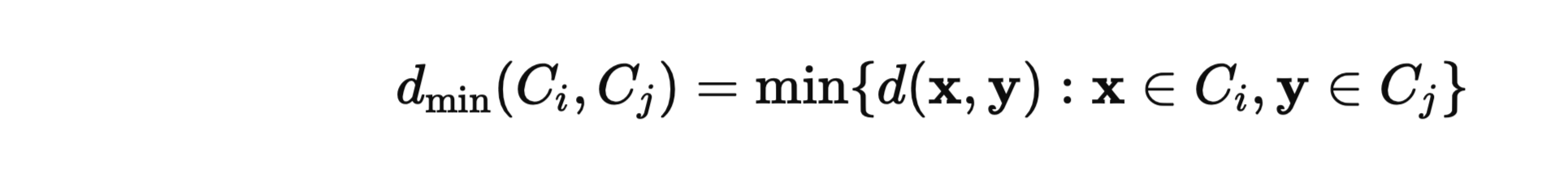
- Merges clusters based on the closest pair of points.
- Complete Linkage (Maximum Distance):
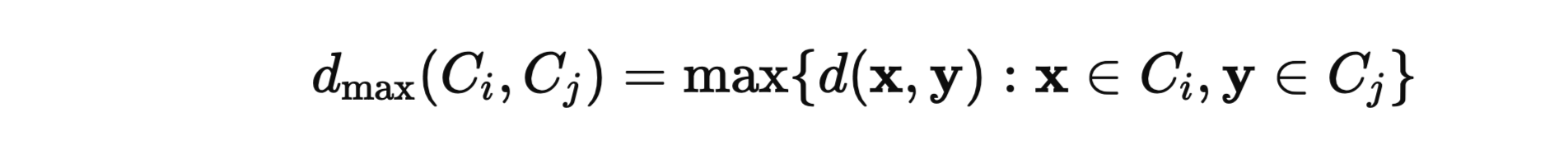
- Merges clusters based on the farthest pair of points.
- Average Linkage:
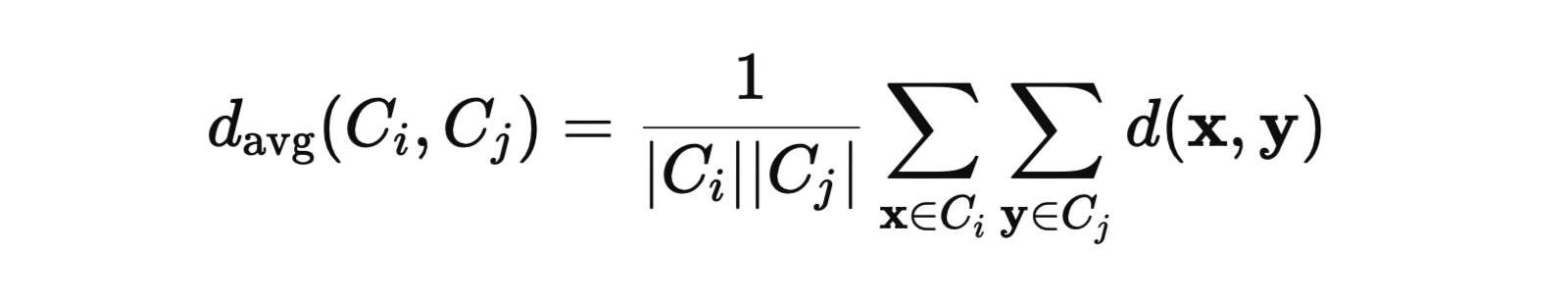
- Considers the average distance between all pairs of points in the two clusters.
- Ward's Method:Ward's method aims to minimize the total within-cluster variance. At each step, the pair of clusters that leads to the minimum increase in total within-cluster variance after merging is selected.
- The distance between two clusters (Ci) and (Cj) is defined as:
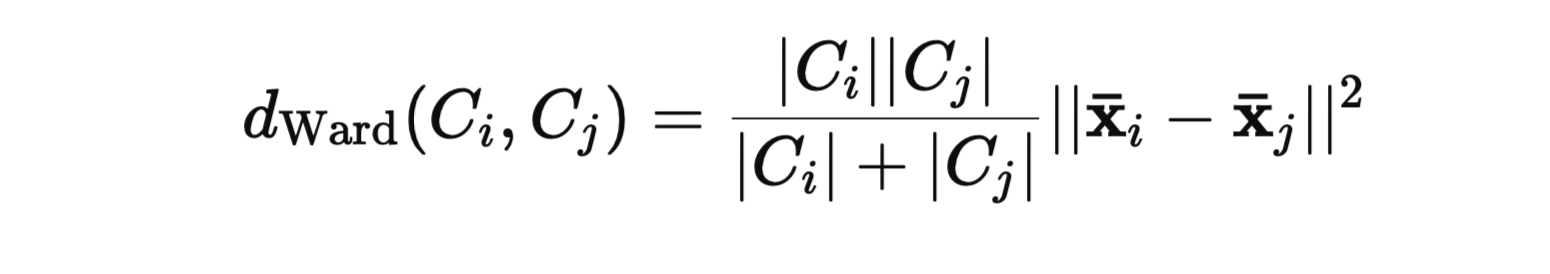
where:
- (|C_i|) and (|C_j|) are the sizes (number of data points) of clusters (C_i) and (C_j), respectively.
- (\mathbf{\bar{x}}_i) and (\mathbf{\bar{x}}_j) are the centroids (mean vectors) of clusters (C_i) and (C_j), respectively
- (|| \cdot ||) denotes the Euclidean norm.
- Objective: Minimize the sum of squared differences within all clusters:

Hierarchical Clustering Algorithm Steps
- Initialization:
- Start with (N) clusters, each containing a single data point.
- Compute Distance Matrix:
- Calculate the distance between every pair of clusters using the chosen linkage criterion.
- Merge Clusters:
- Identify the pair of clusters ((Ci, Cj)) with the smallest distance (d(Ci, Cj)).
- Merge (Ci) and (Cj) into a new cluster (Cij).
- Update Distance Matrix:
- Recompute the distances between the new cluster (Cij) and all other clusters.
- Repeat:
- Repeat steps 3 and 4 until all data points are merged into a single cluster or until a stopping criterion is met (e.g., a predefined number of clusters).
Step 1: Importing the Libraries
First, import the necessary libraries.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
- NumPy: For numerical computations.
- Matplotlib: For plotting graphs and visualizations.
- Pandas: For data manipulation and analysis.
Step 2: Importing the Dataset
Load the dataset and select the features for clustering.
dataset = pd.read_csv('Mall_Customers.csv')
X = dataset.iloc[:, [3, 4]].values
dataset: Loads the CSV file into a DataFrame.X: Extracts the Annual Income and Spending Score columns.
Step 3: Using the Dendrogram to Find the Optimal Number of Clusters
A dendrogram helps visualize the hierarchical merging of clusters and determine the optimal number of clusters.
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method='ward'))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean Distances')
plt.show()
- SciPy's
schmodule: Provides functions for hierarchical clustering. sch.linkage: Computes the linkage matrix using Ward's method.- Ward's method minimizes the total within-cluster variance.
sch.dendrogram: Plots the dendrogram.
Interpretation:
- Cutting the Dendrogram: By drawing a horizontal line across the dendrogram, we can determine the number of clusters.
- Optimal Number of Clusters: Look for the largest vertical distance (called the inconsistency coefficient) that doesn't cross any horizontal lines. The number of vertical lines intersected by the horizontal cut corresponds to the number of clusters.
Step 4: Training the Hierarchical Clustering Model
Based on the dendrogram, choose the number of clusters (e.g., 5) and fit the model.
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(
n_clusters=5, affinity='euclidean', linkage='ward')
y_hc = hc.fit_predict(X)
AgglomerativeClustering: Scikit-learn's class for hierarchical clustering.- Parameters:
n_clusters: The number of clusters to form.affinity: Metric used to compute the linkage (default is 'euclidean').linkage: Specifies the linkage criterion ('ward' minimizes the variance within clusters).
y_hc: An array of cluster labels assigned to each data point.
Note: In scikit-learn versions >= 0.22, the affinity parameter has been deprecated in favor of metric, and you should use metric='euclidean' and linkage='ward'.
Step 5: Visualizing the Clusters
Plot the clusters to see how the data points are grouped.
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1],
s=100, c='red', label='Cluster 1')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1],
s=100, c='blue', label='Cluster 2')
plt.scatter(X[y_hc == 2, 0], X[y_hc == 2, 1],
s=100, c='green', label='Cluster 3')
plt.scatter(X[y_hc == 3, 0], X[y_hc == 3, 1],
s=100, c='cyan', label='Cluster 4')
plt.scatter(X[y_hc == 4, 0], X[y_hc == 4, 1],
s=100, c='magenta', label='Cluster 5')
plt.title('Clusters of Customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()
plt.scatter: Plots data points for each cluster in different colors.- Parameters:
X[y_hc == i, 0]: Selects data points in clusterifor the x-axis.X[y_hc == i, 1]: Selects data points in clusterifor the y-axis.s: Size of the markers.c: Color of the markers.label: Label for the legend.
Visualization Interpretation:
- Cluster 1 (Red): Customers with medium income and medium spending score.
- Cluster 2 (Blue): Customers with high income but low spending score.
- Cluster 3 (Green): Customers with low income but high spending score.
- Cluster 4 (Cyan): Customers with low income and low spending score.
- Cluster 5 (Magenta): Customers with high income and high spending score.
Conclusion
In this tutorial, we:
- Explored hierarchical clustering: Learned about agglomerative clustering and its mathematical foundations.
- Used dendrograms: Determined the optimal number of clusters visually.
- Trained a model: Applied hierarchical clustering to the dataset.
- Visualized the results: Plotted the clusters to interpret the customer segments.
Hierarchical clustering is especially useful when the number of clusters is not known beforehand. It provides a clear visual representation of how clusters are formed, which can be invaluable for exploratory data analysis.
Next Steps:
- Experiment: Try changing the number of clusters or the linkage criteria.
- Feature Scaling: Consider scaling the features if the units are different.
- Other Datasets: Apply hierarchical clustering to different datasets to see how it performs.
References:
- Scikit-learn Agglomerative Clustering Documentation
- SciPy Hierarchical Clustering
- Mall Customers Dataset on Kaggle