Linear Algebra for Machine Learning: A Python Introduction

I apologize for the delay in my posts. I've recently moved from Copenhagen to Boston for a change of scientific environment, and adjusting took some time 😊. Now that I'm settled, I'm excited to share a new blog on Linear Algebra with Python.

When I first started learning Machine Learning using Python, I struggled to understand what was happening behind the scenes. If you've had similar feelings, this blog is for you. Let's dive in together!

Linear algebra is a fundamental area of mathematics that is essential for machine learning and deep learning. It helps in representing data and optimizing algorithms, making it easier to develop and understand complex models. This article offers a straightforward introduction to linear algebra, complemented by practical Python examples to demonstrate key ideas and their applications in machine learning and deep learning.

Table of Contents

1. Why Linear Algebra Matters in Machine Learning
2. Scalars, Vectors, and Matrices
3. Operations on Vectors and Matrices
4. Vector Norms and Distances
5. Systems of Linear Equations
6. Eigenvalues and Eigenvectors
7. Applications in Machine Learning
8. Conclusion

1. Why Linear Algebra Matters in Machine Learning

In machine learning, data is often complex and high-dimensional. Linear algebra provides the tools to handle and manipulate this data effectively. Key applications include:

• Data Representation: Data points and their features are organized as vectors and matrices.
• Model Training: Techniques like linear regression use linear algebra to find the best parameters.
• Dimensionality Reduction: Methods such as Principal Component Analysis (PCA) use linear algebra to reduce the number of features.
• Neural Networks: Operations within neural networks involve multiplying and transforming matrices of weights and activations.

Relevance to Deep Learning

Deep learning models, such as neural networks, rely heavily on linear algebra for operations like forward and backward propagation. Efficient matrix computations enable the training of large-scale models with millions of parameters.

2. Scalars, Vectors, and Matrices

Here are the differences between Scalar, Vector, matrix and tensors:

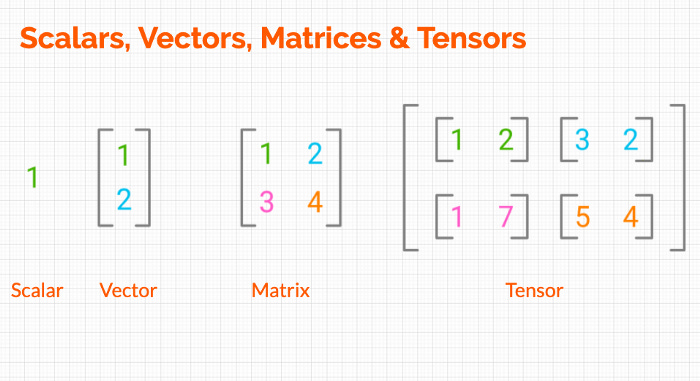
Scalars

A scalar is simply a single number. For example:

# Scalar example
scalar = 5

Relevance in Machine Learning and Deep Learning

Scalars are used to represent single values such as learning rates, loss values, or individual parameters within models.

Vectors

A vector is an ordered list of numbers. It can be visualized as a row or a column. For instance:

import numpy as np

# Vector example
vector = np.array([1, 2, 3])

Relevance in Machine Learning and Deep Learning

Vectors represent data points, feature sets, and parameters in models. For example, input features to a machine learning model are often represented as vectors.

Matrices

A matrix is a two-dimensional array of numbers, organized in rows and columns. Here's how you can create a matrix:

# Matrix example
matrix = np.array([[1, 2], [3, 4], [5, 6]])

Relevance in Machine Learning and Deep Learning

Matrices are used to represent datasets, where each row corresponds to a data sample and each column represents a feature. In deep learning, weight matrices connect layers in neural networks, facilitating the transformation of data as it flows through the network.

3. Operations on Vectors and Matrices

Addition and Subtraction

You can add or subtract vectors and matrices of the same size by performing these operations element-wise.

# Vector addition
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])
vector_sum = vector_a + vector_b

# Matrix subtraction
matrix_a = np.array([[1, 2], [3, 4]])
matrix_b = np.array([[5, 6], [7, 8]])
matrix_diff = matrix_a - matrix_b

Relevance in Machine Learning and Deep Learning

Element-wise operations are fundamental in adjusting model parameters, combining features, and implementing activation functions within neural networks.

Scalar Multiplication

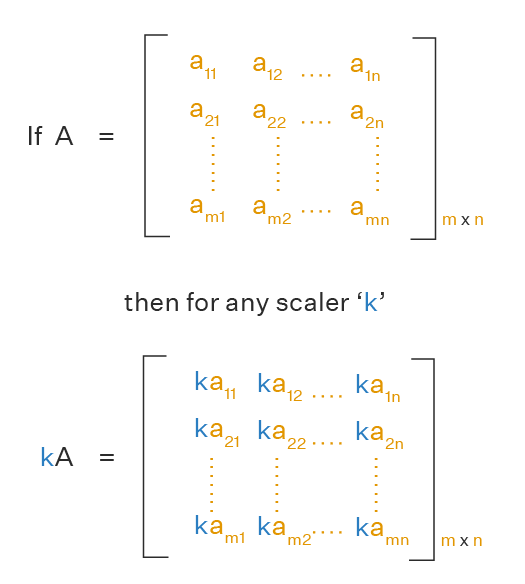
Multiplying a vector or matrix by a scalar means multiplying each element by that number.

# Scalar multiplication
scalar = 2
vector_scaled = scalar * vector_a
matrix_scaled = scalar * matrix_a

Relevance in Machine Learning and Deep Learning

Scalar multiplication is used to scale features, adjust learning rates, and apply regularization techniques that prevent overfitting by penalizing large weights.

Matrix Multiplication

Matrix multiplication combines two matrices by multiplying rows of the first matrix with columns of the second.

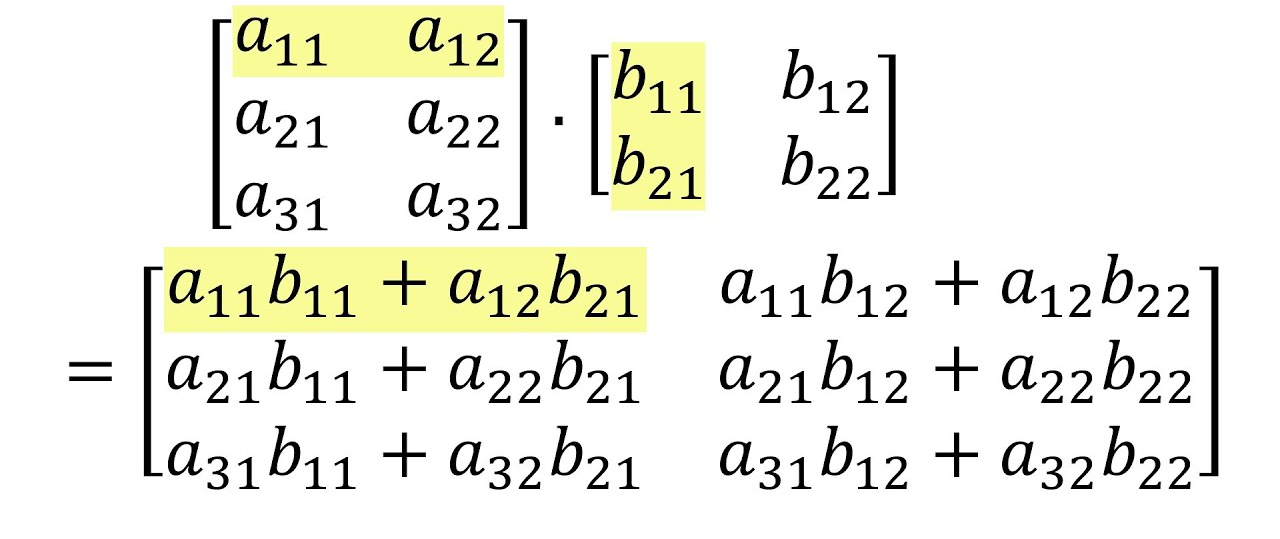
# Matrix multiplication
matrix_a = np.array([[1, 2], [3, 4]])
matrix_b = np.array([[5, 6], [7, 8]])
matrix_c = np.dot(matrix_a, matrix_b)

Relevance in Machine Learning and Deep Learning

Matrix multiplication is essential for propagating inputs through layers in neural networks, transforming data, and performing computations in algorithms like convolutional neural networks (CNNs).

Transpose

Transposing a matrix flips it over its diagonal, switching rows with columns.

# Transpose of a matrix
matrix_transposed = matrix_a.T

Relevance in Machine Learning and Deep Learning

Transposes are used in operations such as calculating covariance matrices in PCA and adjusting dimensions for matrix multiplications in neural network layers.

Dot Product

The dot product of two vectors is the sum of the products of their corresponding elements. "Matrix dot multiplication" is essentially the same as "matrix multiplication" 

# Dot product
dot_product = np.dot(vector_a, vector_b)

Relevance in Machine Learning and Deep Learning

Dot products are fundamental in calculating similarities between vectors, implementing linear transformations, and computing outputs in neural network layers.

4. Vector Norms and Distances

Vector Norms

A vector norm measures the length or size of a vector. Common types include:

• L1 Norm (Manhattan Norm): Sum of the absolute values of the vector's elements.

For a vector v with elements v1,v2,…,vn​:

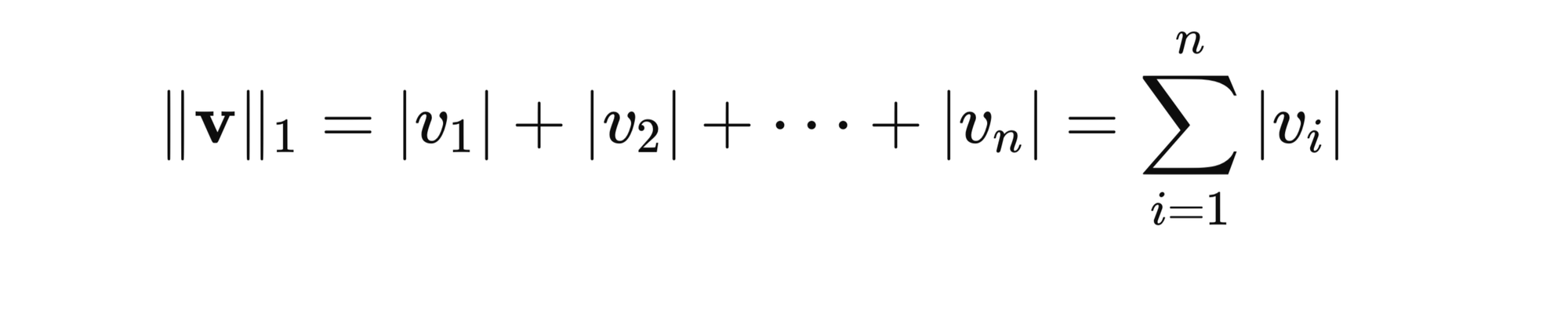
Let’s consider a vector v = [3, -4]

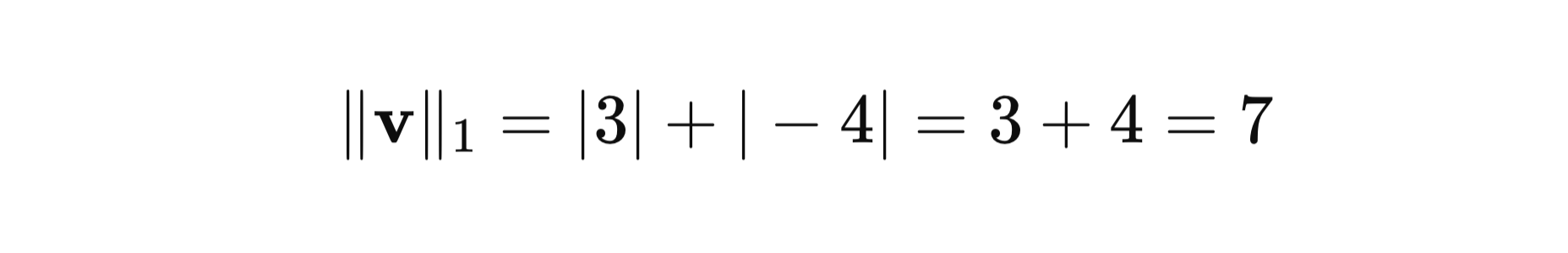
• L2 Norm (Euclidean Norm): The straight-line distance from the origin to the point represented by the vector.

For a vector v with elements v1,v2,…,vn​:

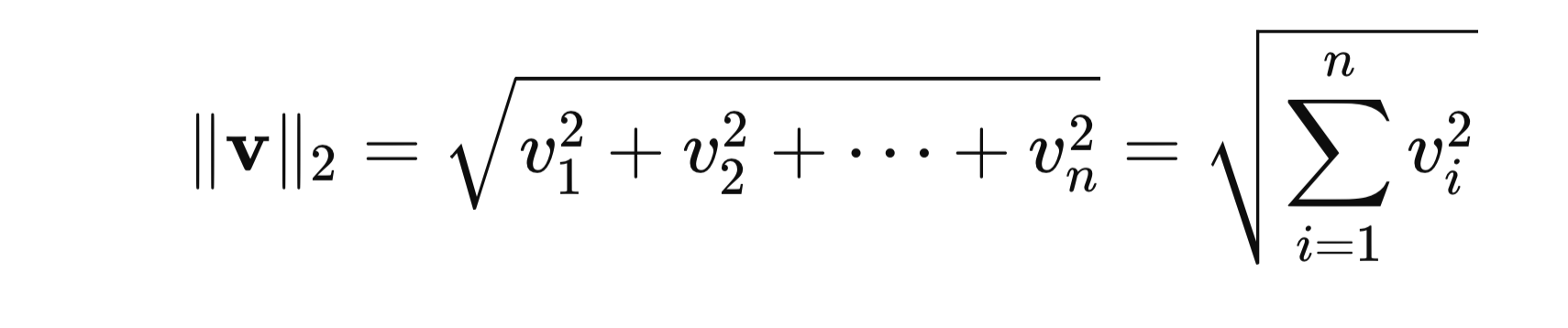
Let’s consider a vector v = [3, -4]

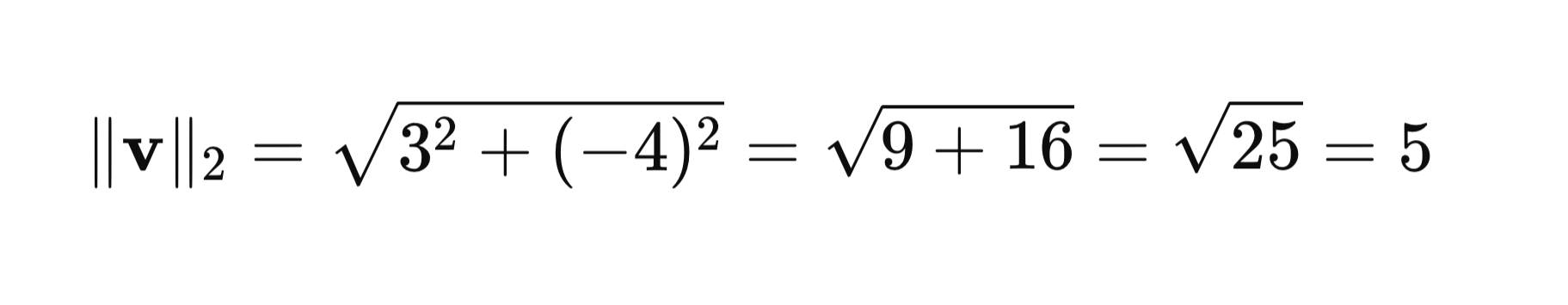
# L1 Norm
l1_norm = np.linalg.norm(vector_a, ord=1)

# L2 Norm
l2_norm = np.linalg.norm(vector_a)

Relevance in Machine Learning and Deep Learning

Norms are used to measure the magnitude of vectors, which is essential in optimization algorithms. They are also used in regularization techniques to prevent overfitting by limiting the size of the model parameters.

Euclidean Distance

Euclidean distance measures how far apart two vectors are in space.

Let's consider two vectors u = [1, 2] and v = [4, 6].

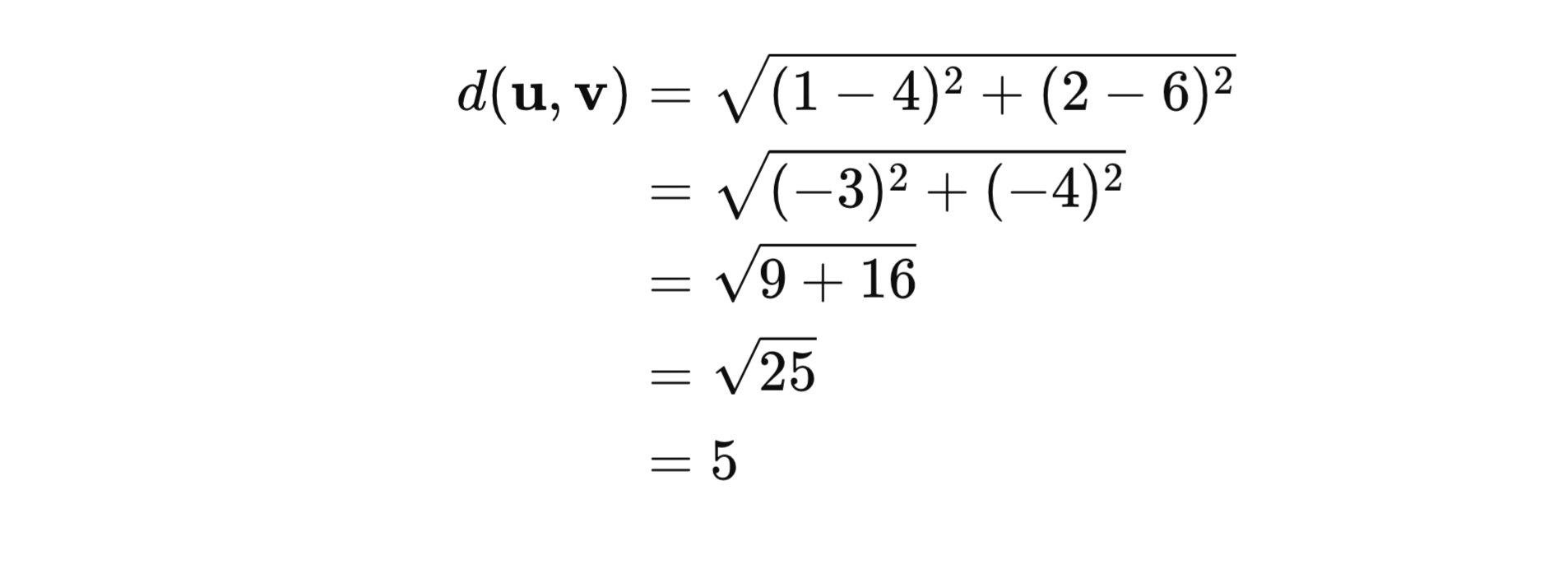
# Euclidean distance
vector_c = np.array([7, 8, 9])
distance = np.linalg.norm(vector_a - vector_c)

Relevance in Machine Learning and Deep Learning

Distance metrics are crucial in algorithms like k-nearest neighbors (KNN), clustering algorithms, and in assessing the similarity between data points or feature vectors.

5. Systems of Linear Equations

Solving systems of linear equations is crucial for optimizing machine learning models.

Solving Equations

Given a matrix of coefficients and a result vector, you can solve for the unknown variables.

# Solving linear equations
A = np.array([[2, 1], [1, 3]])
b = np.array([8, 18])
x = np.linalg.solve(A, b)

Relevance in Machine Learning and Deep Learning

Solving linear equations is fundamental in algorithms like linear regression, where the goal is to find the best-fit parameters that minimize the error between predicted and actual values.

Inverse of a Matrix

The inverse of a matrix allows you to solve equations by reversing the matrix operations.

# Inverse of a matrix
A_inv = np.linalg.inv(A)

Relevance in Machine Learning and Deep Learning

Matrix inverses are used in calculating optimal parameters in linear regression through the normal equation and in various optimization algorithms that require matrix manipulation.

6. Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors help in understanding how matrices transform space, which is important for many machine learning algorithms.

Definitions

• Eigenvector: A vector that only changes in scale when a matrix is applied to it.
• Eigenvalue: The factor by which the eigenvector is scaled.

Mathematical Example

# Eigenvalues and eigenvectors
eig_values, eig_vectors = np.linalg.eig(A)

Relevance in Machine Learning and Deep Learning

Eigenvalues and eigenvectors are crucial in dimensionality reduction techniques like PCA, which identify the principal components that capture the most variance in the data. They also play a role in understanding the behavior of optimization algorithms and the stability of neural networks.

Importance in PCA

In Principal Component Analysis (PCA), eigenvectors determine the directions of maximum variance in the data, while eigenvalues indicate the importance of these directions.

7. Applications in Machine Learning

Linear Regression

Linear regression predicts a continuous outcome by fitting a line to the data using linear algebra techniques.

# Linear regression using normal equation
X = np.array([[1, 1], [1, 2], [1, 3]])  # Adding bias term
y = np.array([1, 2, 3])

# Normal equation: w = (X^T X)^-1 X^T y
w = np.linalg.inv(X.T @ X) @ X.T @ y

Relevance in Machine Learning and Deep Learning

Linear regression is one of the simplest machine learning algorithms and serves as a foundation for more complex models. Understanding its linear algebra underpinnings helps in grasping how models learn from data.

Dimensionality Reduction with PCA

PCA reduces the number of features in your data by projecting it onto the most important directions.

from sklearn.decomposition import PCA

# Sample data
data = np.array([[2.5, 2.4],
                 [0.5, 0.7],
                 [2.2, 2.9],
                 [1.9, 2.2],
                 [3.1, 3.0],
                 [2.3, 2.7],
                 [2, 1.6],
                 [1, 1.1],
                 [1.5, 1.6],
                 [1.1, 0.9]])

# Applying PCA
pca = PCA(n_components=1)
principal_components = pca.fit_transform(data)

Relevance in Machine Learning and Deep Learning

PCA is used to reduce the dimensionality of data, which can help improve the performance of machine learning models by eliminating noise and reducing computational complexity. It also aids in data visualization and feature engineering.

Neural Networks

Neural networks use linear algebra to transform inputs through layers using weight matrices and activation functions.

# Simple neural network layer
def neural_layer(input_vector, weight_matrix, bias_vector):
    return np.maximum(0, np.dot(input_vector, weight_matrix) + bias_vector)  # ReLU activation

# Example usage
input_vector = np.array([0.5, 0.2])
weight_matrix = np.array([[0.1, 0.3], [0.4, 0.6]])
bias_vector = np.array([0.1, 0.2])
output = neural_layer(input_vector, weight_matrix, bias_vector)

Relevance in Machine Learning and Deep Learning

Neural networks consist of multiple layers of neurons, each performing linear transformations followed by non-linear activations. Efficient matrix operations enable the training of deep networks, allowing them to learn complex patterns and representations from data.

Additional Applications in Deep Learning

• Convolutional Neural Networks (CNNs): Utilize matrix operations for filtering and pooling in image processing tasks.
• Recurrent Neural Networks (RNNs): Employ matrix multiplications to handle sequential data and maintain hidden states.
• Transformer Models: Rely on matrix operations for attention mechanisms that capture relationships between different parts of the input data.

8. Conclusion

Linear algebra is essential for understanding and building machine learning and deep learning algorithms. It provides the necessary tools to work with vectors and matrices, solve equations, and perform complex transformations. From basic operations to advanced concepts like eigenvalues and eigenvectors, linear algebra enables the manipulation and interpretation of high-dimensional data.

By mastering these basics, you'll be well-equipped to explore more advanced machine learning and deep learning topics, develop efficient algorithms, and contribute effectively to advancements in the field.

Further Reading

Here are two amazing books, that can help you brush your concepts.

• Linear Algebra and Its Applications by Gilbert Strang
• Deep Learning Book by Ian Goodfellow et al.